欧拉:数学史上的巨人与科学的百科全书
欧拉:数学史上的巨人与科学的百科全书
在数学和科学的历史长河中,有许多杰出的人物为人类知识的积累做出了卓越的贡献。而瑞士数学家莱昂哈德·欧拉(Leonhard Euler,1707—1783)无疑是其中最璀璨的明星之一。他不仅是一个数学天才,更是一个知识的百科全书,其成就横跨数学、物理学、天文学等多个领域。本文将带您走进欧拉的世界,探讨他的生平、主要贡献以及他对后世的深远影响。
一、欧拉的生平与背景
莱昂哈德·欧拉于1707年出生在瑞士巴塞尔的一个牧师家庭。他的父亲是一位知识渊博的神学家,欧拉从小便受到良好的教育。早年,他在巴塞尔大学学习,师从著名的数学家约翰·伯努利。在伯努利的指导下,欧拉展现出了非凡的数学天赋。
1727年,欧拉前往圣彼得堡,成为俄罗斯科学院的成员。在那里,他不仅从事数学研究,还参与了许多与物理和工程相关的项目。后来的几年中,欧拉多次往返于瑞士和俄罗斯,直至最终定居于圣彼得堡。他的职业生涯中,尽管遭遇了许多个人挑战,包括失去视力,但他依然保持着高产的创作状态,撰写了大量的学术论文和著作。

二、函数符号的创立
欧拉在数学符号化方面的贡献尤为重要。他是第一个系统性地使用“函数”这个术语的人,并创立了许多数学符号,包括常用的“f(x)”表示函数的形式。这一创新不仅使数学表达更加简洁明了,也为后来的数学家提供了强有力的工具,极大地推动了数学的发展。
例如,欧拉引入了“e”作为自然对数的底数,这一符号在后来的数学分析中成为了基础概念。他的这些符号化工作,使得复杂的数学概念变得更加易于理解和应用,为现代数学的建立奠定了基础。
三、分析力学的奠基
欧拉在物理学领域的贡献同样不可小觑。他创立了分析力学,为经典力学的发展奠定了理论基础。欧拉的《分析力学》一书,系统地总结了力学的基本原理,并引入了拉格朗日方程,这一方法至今仍在现代物理和工程中广泛应用。
在这部作品中,欧拉将运动的描述从直观的几何方法转向了更为抽象的数学方法,极大地提升了物理学的数学化程度。他的分析力学理论不仅影响了后来的科学家,如拉格朗日和哈密顿,也为后来的现代物理学奠定了基础
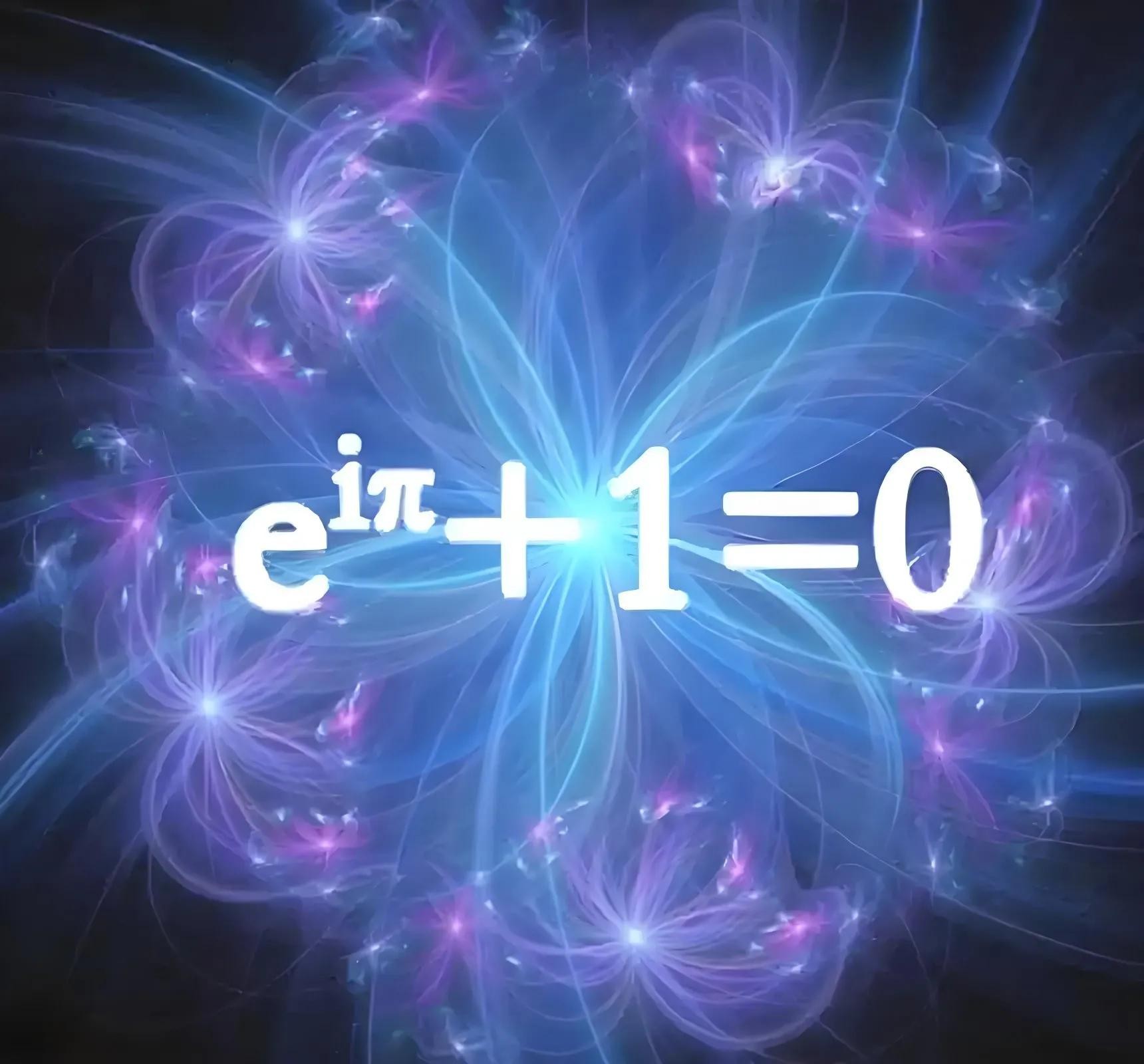
。
四、柯尼斯堡七桥问题的解决
柯尼斯堡七桥问题是欧拉在图论方面的开创性工作。这个问题源于18世纪的柯尼斯堡(今加里宁格勒),当时的城市被两条河流分隔,七座桥连接着城市的不同部分。问题是:是否可以从城市的一个点出发,经过每座桥一次且仅一次,最终回到起点?
欧拉在1736年发表的论文中,首次提出了图论的基本概念,并证明了这个问题没有解。他的研究不仅解决了当时的难题,也为图论的发展奠定了基础。今天,图论在计算机科学、网络分析等领域中发挥着重要作用,而这一切都可以追溯到欧拉的伟大工作。
五、欧拉公式的辉煌
欧拉公式是数学中最美丽的公式之一,通常表示为:
[ e^{ix} = \cos(x) + i\sin(x) ]
这个公式将数学中的五个基本常数(e、i、π、1和0)巧妙地联系在一起,展现了数学的和谐美。欧拉的这一发现不仅在数学理论上具有深远的意义,也在工程、物理等领域中得到了广泛应用。
此外,欧拉还提出了多个重要的公式和定理,如欧拉定理、欧拉路和欧拉图等。这些理论在数学的多个分支中都有重要的应用,成为后世数学家研究的基础。

六、主要著作与影响
欧拉一生创作了大量的学术著作,涵盖了数学、物理学、天文学等多个领域。他的主要著作包括《无穷小分析引论》和《微分学原理》等,这些作品在当时和后来的数学研究中都产生了深远的影响。
欧拉的研究方法严谨而系统,他的许多成果至今仍然是数学教学和研究的重要内容。他的著作不仅为后来的数学家提供了宝贵的参考资料,也激励了无数后继者在科学探索的道路上不断前行。
七、结语:欧拉的遗产
莱昂哈德·欧拉以其卓越的才华和不懈的努力,成为了数学史上的一座丰碑。他的贡献不仅体现在他所创造的理论和公式上,更在于他所开创的研究方法和思维方式。今天,欧拉的名字仍然在数学、物理等多个领域中被频繁提及,他的成就将永远铭刻在科学史册上。
欧拉的故事告诉我们,科学的探索是一个不断创新和发展的过程。无论是在数学的深海中,还是在科学的广阔天地里,欧拉的精神激励着一代又一代的科学家,推动着人类知识的不断进步。让我们铭记这位伟大的数学家,继续在探索真理的道路上勇往直前!
-

- “冰清玉洁”四姐妹成反面教材,与南京“四小凤”,差距越拉越大
-
2025-10-19 03:27:33
-
- 东风本田哥瑞上市 售价7.98万~11.98万元
-
2025-10-19 03:25:18
-

- 一个是“努尔哈赤后人”,一个来自“浙音明星班”,这届好声音很有故事
-
2025-10-19 03:23:03
-

- 刘诗诗电视剧被佟大为强行抱起,注意她的脚?舞蹈演员的基本素养
-
2025-10-18 21:40:16
-

- 24岁武汉研究生为省1000块钱离世,救了4人,残父幼妹却孤苦无依
-
2025-10-18 21:38:01
-

- 8月运(上升狮子座):当下,工作方面一定要稳妥为主
-
2025-10-18 21:35:46
-

- 永远的痛:中驻南使馆被炸,中国的忍耐和烈士的牺牲绝不会被辜负
-
2025-10-18 21:33:31
-

- 深度科普东南亚国家文莱
-
2025-10-18 21:31:17
-

- 山东省济北中学家庭教育年度工作汇报展示
-
2025-10-18 21:29:02
-

- 美国最蠢总统,拿了一手好牌的小布什,如何把美国从巅峰带入危机
-
2025-10-18 21:26:47
-

- 最新预测!春节期间,这些高速路段易拥堵
-
2025-10-18 21:24:32
-

- 得帆云X银雁科技,低代码筑基,AIGC赋能,共创数字化转型新路径
-
2025-10-18 21:22:17
-

- 写在FIX字幕侠成立五周年之际
-
2025-10-18 21:20:02
-

- 《鹿鼎记》神龙教和天地会谁在江湖上的势力更大?当然是天地会
-
2025-10-18 05:57:47
-

- 欧洲杯往事,2000年欧锦赛最佳12-22号球员阵容,意大利6人入选
-
2025-10-18 05:55:32
-

- 李光耀晚年直言:新加坡虽是华人国家,但不会“回归祖国”
-
2025-10-18 05:53:16
-
- 出狱后的赖文峰:娶小23岁年轻娇妻,素颜照惊艳全网!
-
2025-10-18 05:51:02
-
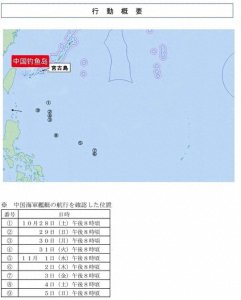
- 9天570架次,日本公布“山东”舰数据,出动能力赶上美军航母了?
-
2025-10-18 05:48:47
-

- 希腊神话之阿喀琉斯:无人能敌的英雄也有死穴?
-
2025-10-18 05:46:32
-

- 这十大全国神仙美术馆,也太美了吧
-
2025-10-18 05:44:17


 以前很红的歌星卫兰,为何突然销声匿迹了?
以前很红的歌星卫兰,为何突然销声匿迹了? 网传将鄂州并入武汉,城市体量小,又是都市圈副城等都是关键因素
网传将鄂州并入武汉,城市体量小,又是都市圈副城等都是关键因素